Ecuaciones Lineales: Definición, Ejemplos y Sistemas
Definición de Ecuación Lineal
Una ecuación lineal es una expresión matemática que establece una relación de igualdad (por eso la palabra ‘ecuación’) entre dos expresiones, donde cada término es una constante o el producto de una constante por una variable de primer grado (esto es la linealidad).
La forma general de una ecuación lineal con dos variables es:
[math]ax + by = c[/math]
Donde [math]a[/math], [math]b[/math], y [math]c[/math] son constantes reales, y [math]x[/math] e [math]y[/math] son variables.
Si quisieras una ecuación lineal con 5 variables, su forma general sería:
[math]a_1 x_1+a_2x_2+a_3 x_3 +a_4 x_4 +a_5 x_5 = b[/math]
Donde las [math]x_i[/math] son las variables y las [math]a_i[/math] y el lado derecho [math]b[/math] son constantes.
Entonces, características clave:
| Característica | Descripción |
|---|---|
| Grado | Siempre es 1 para cada variable |
| Variables | Pueden tener una o más variables |
| Exponentes | Las variables nunca tienen exponentes distintos de 1 |
| Productos | No hay productos entre variables (un termino como [math]xy[/math] daña la linealidad) |
Ejemplos de Ecuaciones Lineales
- [math]2x + 3y = 10[/math]
- [math]-5x + 2y – z = 7[/math]
- [math]3.5x – 2.1y = 0[/math]
- [math]x = 5[/math] (aunque sea una sola variable, esto es lineal)
- [math]3.5^2x – \sqrt{2+sin(3)}y = 0[/math] (esto lo pongo para confundirte, las constantes siguen siendo constantes aun estando en funciones no lineales como el seno o la raíz cuadrada, lo que importa es que LAS VARIABLES estén en grado 1).
Ejemplos de Ecuaciones NOoooo Lineales
- [math]2x^2 + 3y = 10[/math]
- [math]-5xy – z = 7[/math]
- [math]3.5x^{\frac{1}{2}} – 2.1y = 0[/math]
- [math]\log(x) = 5[/math]
Sistemas de Ecuaciones Lineales
Un sistema de ecuaciones lineales es un conjunto de dos o más ecuaciones lineales que se resuelven simultáneamente. Los sistemas pueden tener diferentes tipos de soluciones:
Este fenómeno de los tipos de soluciones es el corazón del Algebra Lineal. Para todo sistema lineal, hay tres posibilidades, y tu entrenamiento será justamente indentificarlos en muchos contextos.
1. Sistema con Única Solución
2x + y = 5
x - y = 1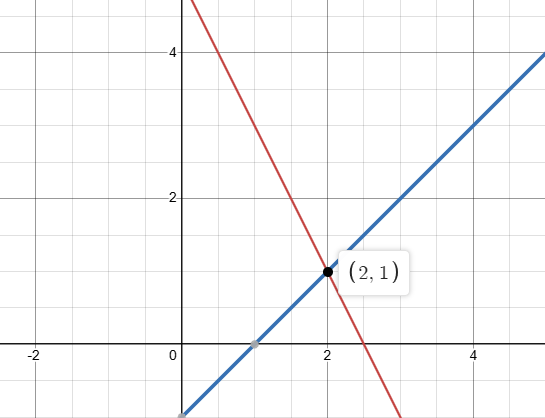
Solución: [math]x = 2[/math], [math]y = 1[/math]
Este sistema tiene una única solución porque las ecuaciones representan rectas que se intersectan en un solo punto.
2. Sistema con infinitas soluciones
2x + y = 5
4x + 2y = 10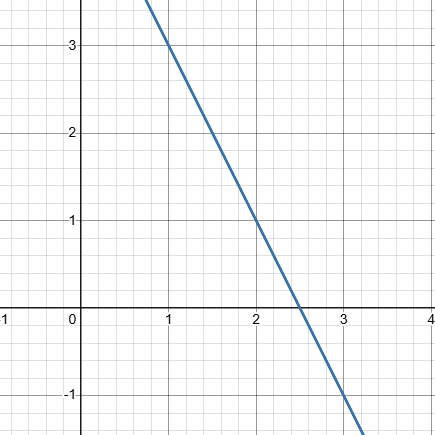
En el gráfico ambas son la misma. Este sistema tiene infinitas soluciones porque las ecuaciones representan la misma recta. Cualquier par [math](x, y)[/math] que satisfaga una ecuación también satisfará la otra.
3. Sistema sin solución
2x + y = 5
2x + y = 7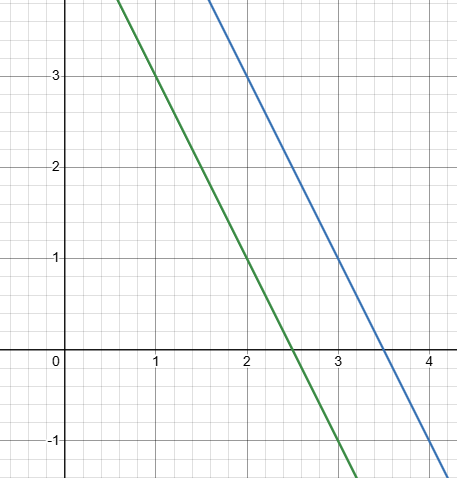
Este sistema no tiene solución porque las ecuaciones representan rectas paralelas que nunca se intersectan.
Resumen de Tipos de Soluciones
| Tipo de Solución | Interpretación Geométrica (una de las tantas interpretaciones geométricas) | Comentarios |
|---|---|---|
| Única | Rectas que se intersectan en un punto | Veremos muchas maneras de caracterizar (lo que significa formas de identificar) este caso. Es el caso que más ‘nos gusta’, ya que da una sola solución. |
| Infinitas | Rectas coincidentes | Puedes mirar que las ecuaciones aunque parecen ‘distintas’ son en realidad la misma. Tienen la misma información, hay cierta redundancia. |
| Ninguna | Rectas paralelas que no son coincidentes | Sistema inconsistente. Inconsitente significa que lleva en sí mismo alguna contradicción, algo imposible. |
Ejemplo Práctico:
Sistema de Ecuaciones con Muchas Variables
En la práctica, los ingenieros y científicos a menudo se enfrentan a sistemas de ecuaciones con numerosas variables. Por ejemplo, en el análisis de redes eléctricas complejas, podríamos encontrar un sistema como este:
2.1v1 - 0.3v2 + 0.1v3 + 0.5v4 - 0.2v5 + ... + 1.7v50 = 10
-0.3v1 + 3.2v2 - 0.4v3 - 0.1v4 + 0.6v5 + ... - 0.9v50 = 5
...
0.7v1 + 0.2v2 + 0.8v3 - 0.3v4 + 0.5v5 + ... + 2.1v50 = 8Este sistema tiene 50 variables ([math]v1[/math] a [math]v50[/math]) y 50 ecuaciones. Resolver tal sistema manualmente sería extremadamente tedioso y propenso a errores, por lo que se utilizan métodos computacionales para encontrar las soluciones.

